Stijn Vermeeren: Blog: International Choice of Urinal Protocol

Blog: International Choice of Urinal Protocol

Donderdag 1 oktober 2009, 18:30

Over de heren-wc zijn er natuurlijk al bibliotheken volgeschreven. Maar er is iemand van het kaliber van Randall Munroe (xkcd) voor nodig om er een interessant wiskundig probleem in te vinden. Randall heeft enkele weken geleden op zijn blag het "International Choice of Urinal Protocol" beschreven:

It’s discussed at length elsewhere, but the basic premise is that the first guy picks an end urinal, and every subsequent guy chooses the urinal which puts him furthest from anyone else peeing. At least one buffer urinal is required between any two guys or Awkwardness ensues.

Als er zeven urinoirs op een rij staan, gaat de eerste man dus aan het eerste urinoir staan, de volgende aan het zevende, en de derde gaat in het midden aan urinoir nummer vier staan. Vervolgens is er geen enkele plek met voldoende privacy meer vrij, tot grote ergernis van de volgende wc-bezoeker die de rest vervloekt omdat er in principe vier personen aan zeven urinoirs kunnen staan met steeds ruimte ertussen.

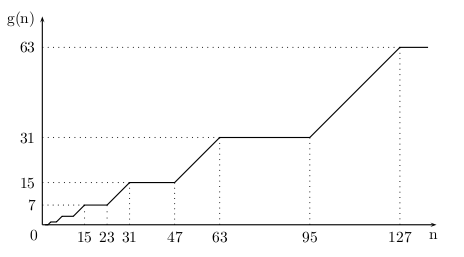
Randall Munroe heeft de efficiëntie van dit protocol onderzocht. Voor n urinoirs, hoeveel worden er maximaal ingenomen? Randall geeft de volgende formule:

$LaTeX: f(n) = 1 + 2^{\lfloor \log_2 (n-2) - 1\rfloor} + \max \left(0, n-\frac{3}{2} 2^{\lfloor \log_2 (n-2) \rfloor} -1 \right).$

Een akelige uitdrukking die hij waarschijnlijk blindelings uit een computeralgebra-pakket heeft overgenomen. Helaas, want een nauwkeurige afleiding van de formule leidt tot interessante wiskunde, met name tot de boeiende recursieve vergelijking

$LaTeX: g(1) = g(2) = 0$

$LaTeX: g(n) = g\left(\left\lfloor \frac{n-1}{2} \right\rfloor \right) + g\left(\left\lceil \frac{n-1}{2} \right\rceil \right) + 1$

waarbij $LaTeX: g(n) = f(n+2) - 2$ de twee uiterste urinoirs negeert, een iets elegantere benadering. Met een beetje zoekwerk vind je dat

$LaTeX: g(n) = \max\left( 2^{k-1} - 1, l \right)$

waarbij $LaTeX: n = 2^k + l$ met $LaTeX: 0 \leq l < 2^k$ . Heel wat eleganter dan Randalls formule, niet?

Grafiek van g(n)

De "packing efficiency" van het protocol is het percentage van de urinoirs dat maximaal bezet wordt, i.e. g(n)/n. Deze stuitert heen een weer tussen een lim inf van 1/3 en een lim sup van 1/2. De locale maxima worden bereikt voor $LaTeX: n=2^k + 2^k-1$ , waarvoor

$LaTeX: g(n) = \frac{1}{2} - \frac{1}{2n}.$

De locale minima worden bereikt voor $LaTeX: n=2^k + 2^{k-1} - 1$ , waarvoor

$LaTeX: g(n) = \frac{1}{3} - \frac{2}{3n}.$

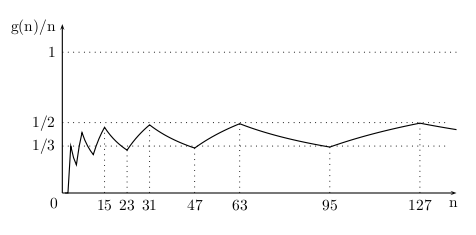
Grafiek van g(n)/n

Opvallend is dat mijn g(n) zijn lim inf en lim sup langs onder benadert, terwijl de benadering bij Randall Munroe's f(n) langs boven gebeurt.

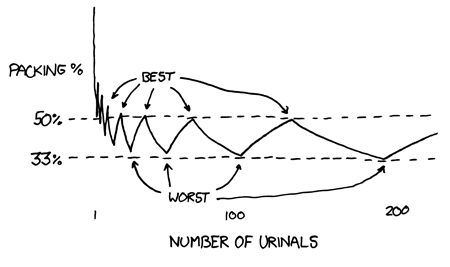
Grafiek van f(n)/n

Moeten toiletarchitecten hier nu mee rekening gaan houden? Neen, in werkelijkheid spelen veel andere factoren mee, zoals het continu komen en gaan van toiletgasten en lagere kinderurinoirs. Maar het mooie aan dit stukje wiskunde is dat het een boeiend probleem is dat toch rechtstreeks uit het dagelijkse leven komt. Wiskunde is overal - zelfs in de toiletten!