Stijn Vermeeren

Het doorsnee wiskundetijdschrift is geen lectuur die je voor het plezier gaat lezen. De artikels die erin staan zij zo technisch en gespecialiseerd dat meestal slechts een handvol mensen ze kan begrijpen. Normaal neem je dus enkel een tijdschrift ter hand als je op zoek bent naar een bepaald artikel waarvan je op voorhand weet dat het relevant zal zijn. Een uitzondering op deze regel is de Mathematical Intelligencer. Dit driemaandelijks tijdschrift publiceert breed toegankelijke artikels, met veel aandacht voor puzzels en recreatieve wiskunde, geschiedenis, en ook wiskundige humor. De Mathematical Intelligencer neem elke keer ik met plezier ter hand.

Minesweeper Consistency

"Minesweeper is NP-complete" is een artikel door de Britse wiskundige Richard Kaye dat in 2000 in de Mathematical Intelligencer verscheen. Inderdaad, het gaat hier enerzijds over het computerspelletje Mijnenveger, en anderzijds over de NP complexiteitsklasse, het onderwerp van een van de $1.000.000 Millennium Prize Problems. Het mag geen verrassing heten dat het artikel dan ook heel wat aandacht kreeg. Ian Stewart besteedde er zelfs een van zijn populaire columns in de Scientific American aan. Die column is in lichtjes gewijzigde vorm (lees: een kemel van een verwarring tussen NP en NP-volledig eruit gehaald) online te vinden.

Wat lezen we nu in de meest recente uitgave en de Mathematical Intelligencer? Een artikel door Allan Scott, Ulrike Stege en (de Nederlandse) Iris van Rooij, getiteld "Minesweeper May Not Be NP-Complete but Is Hard Nontheless". Wat is dat nu? Zat er een fout in het artikel van Richard Kaye? Ian Stewart die NP en NP-volledig verwart is geen grote schok, maar dat er een significante fout zou zitten in Richard Kaye's originele artikel zou wel onthutsend zijn.

Gelukkig gaat het niet over een fout van Richard Kaye, wel over een verschillende interpretatie van het probleem.

Richard Kaye bekijkt het Minesweeper Consistency probleem. Dit gaat als volgt:

• Invoer: een gedeeltelijk onthuld Minesweerper bord (sommige vakjes tonen het aantal omliggende mijnen, sommige vakjes hebben een vlag om te markeren dat er een bom onder ligt, en andere vakjes zijn nog verhuld.)
• Uitvoer: "ja" als het bord consistent is, anders "neen"

Consistent wil zeggen dat er een oplossing bestaat, dus dat je de bommen zodanig kunt verdelen dat alle onthulde cijfertjes en alle reeds gemarkeerde bommen kloppen. Een bord met het cijfertje nul op een vakje naast een bom, is noodzakelijk inconsistent. Maar een bord kan ook op veel subtielere manieren inconsistent zijn.

Bestaat er een algoritme dat "Minesweeper Consistency" efficiënt oplost? Richard Kaye zegt van neen. Toch niet als de klassen P en NP verschillen. Dat bewijzen is het onderwerp van het Millennium Prize Problem. Maar zelfs zonder bewijs denken de meeste wiskundigen en informatici dat P en NP verschillend zijn. P is namelijk de klasse van ja/nee-problemen die efficient (d.w.z. in veeltermtijd) kunnen beantwoord worden. NP (voor "niet-deterministisch polynomiaal") is de klasse van ja/nee-problemen waarbij als het antwoord "ja" is, er een certificaat bestaat dat je er efficiënt van overtuigt dat het antwoord inderdaad "ja" is. Beschouw bijvoorbeeld het probleem "heeft deze legpuzzel een oplossing?". Als het antwoord "ja" is, dan kan je daar gemakkelijk van overtuigd worden door de opgeloste puzzel te zien. Die opgeloste puzzel is het certificaat. Maar als het antwoord "neen" is, dan ben je daar niet zo snel van overtuigd. De enige manier is om de puzzel proberen op te lossen door alle combinaties uit te proberen. Als er een puzzelstukje ontbreekt, dan kom je daar meestal pas achter als na veel werk, als de andere puzzelstukjes reeds op hun plaats liggen. Erg frustrerend, maar er bestaat vrijwel geen manier om na te gaan of de puzzel wel oplosbaar is, zonder de oplossing ook echt proberen te maken. Dat is de intuïtie achter het begrip van een probleem in NP.

Minesweeper Consistency is in NP, want een plaatsing van alle mijnen die met de reeds getoonde gegevens overeenstemt, is een certificaat dat de consistentie bewijst. Voor inconsistente borden schijnt er echter geen certificaat te bestaan, dat je van die inconsistentie overtuigt.

Logische circuits op mijnenvelden

De interessantere kant van Richard Kaye's artikel is echter dat Minesweeper Consistency bij de moeilijkste problemen in NP hoort, de zogenaamde NP-volledige problemen. Dit doet Kaye door aan te tonen dat Minesweeper Consistency minstens even moeilijk is als een gekend NP-volledig probleem, namelijk SAT. SAT (voor "Satisfiability") kan geformuleerd worden met behulp van logische circuits. Een logisch circuit heeft verschillende aan/uit-invoersignalen, die door bepaalde logische poorten (AND, NOT, ...) verwerkt worden tot één aan/uit-uitvoersignaal. SAT is dan de vraag: "bestaat er een combinatie van invoersignalen zodat de uitvoer 'aan' is?". Merk op dat die invoer een "certificaat" is voor een "ja"-antwoord. Maar om een "nee"-antwoord te controleren, kan je schijnbaar niets efficiënter doen dan alle mogelijke invoer-combinaties na te gaan, wat voor grotere circuits al snel onmogelijk veel werk is. Inderdaad, SAT is niet alleen gekend als NP probleem, maar ook als een van de moeilijkste NP problemen, een NP-volledig probleem dus.

Kaye toont aan dat Minesweeper Consistency minstens even moeilijk is als SAT (en dus ook NP-volledig) door SAT te reduceren tot Minesweeper Consistency. Dit wil zeggen dat elke SAT-vraag wordt omgevormd tot een equivalente vraag over de consistentie van een mijnenvegerbord. Dit gebeurt door een geniale codering van logische circuits op mijnenvelden. Een signaal wordt hierbij als volgt over het bord voortgebracht:

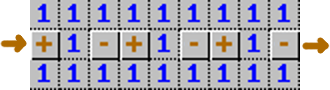
Deze draad draagt een signaal van links naar rechts. Er zijn telkens twee verhulde vakjes naast elkaar, waarover de opliggende cijfertjes bepalen dat juist één van de twee een mijn bevat, en steeds het hetzelfde vakje. Als steeds het eerste -""-vakje een mijn bevat, dat interpreteren we dat als een "uit"-signaal. Als steeds het tweede "+"-vakje een mijn bevat, dan draagt de draad een "aan"-signaal.

Vervolgens moeten we deze mijnenvegerdraden samenvoegen met logische poorten. Bijvoorbeeld een AND-poort:

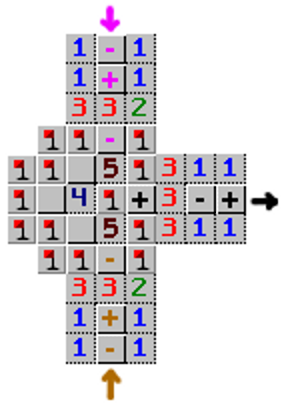
Er komt een "paars" signaal van boven en een "geel" signaal van beneden, die worden samengevoegd tot een "zwart" uitvoersignaal. De nummers 5 zorgen ervoor dat het uitvoersignaal "aan" kan zijn als en slechts als beide invoersignalen ook "aan" zijn. De drie verhulde vakjes rond het cijfer 4 zorgen ervoor dat het geheel een (en niet meer dan één) oplossing heeft voor elke invoer. (Merk op dat juist één van die drie vakjes een bom moet bevatten. Het vakje links van het cijfer 4 zal een bom bevatten als beide invoeren hetzelfde zijn. Anders zal de bom boven of onder de 4 liggen, aan de kant van de "aan"-invoer.)

Deze AND-poort heb ik overigens zelf ontdekt. Ze is kleiner en eleganter dan de oorspronkelijke AND-poort in Richard Kaye's eigen artikel. Reden te meer dus voor de lezer om zelf een beetje te gaan puzzelen om andere elementen van logische circuits in Minesweeper te ontwerpen, want we hebben nog minstens een NOT-gate nodig, elementen om draden te buigen en te kruisen, om een signaal te splitsen...

Dat alles is echter niet meer dan een leuke oefening. Uiteindelijk kunnen we elk logisch circuit coderen in een mijnenvegerbord. Dan moeten we enkel het uitvoersignaal op "aan" zetten, en het mijnenvegerbord is consistent als en slechts als het logisch circuit satisfiable is. Dus Minesweeper Consistency is NP-volledig!

Tot zover Kaye's leuke artikel. Maar welk probleem hebben Scott, Stege en Van Rooij daar nu bij gevonden?

Minesweeper Inference

Wel, zij beweren dat Minesweeper Consistency helemaal niet de juiste vraag is. Je speelt Minesweeper niet door steeds te vragen "is dit bord consistent?" De vraag die je je stelt bij het oplossen is: "kan ik uit de reeds onthulde (consistente) gegevens afleiden of er een bom ligt onder dit vakje?". Of algemener: "Kan ik überhaupt nog iets afleiden uit het reeds onthulde?". Deze twee problemen vallen allebei onder de naam Minesweeper Inference.

Wat blijkt? Deze problemen zijn niet in NP... maar wel in co-NP! Dat wil zeggen, nu bestaat er juist een certificaat als het antwoord " neen" is, maar waarschijnlijk niet als het antwoord "ja" is! Immers: als de inhoud van een vakje niet logisch afgeleid kan worden, dan kan je daarvan overtuigd worden door twee mogelijke oplossingen voor het hele bord te zien te krijgen, waarbij er een bom ligt onder het vakje in de ene oplossing, en niet in de andere.

Meer nog: Scott, Stege en Van Rooij gebruiken helemaal hetzelfde idee als Richard Kaye (de codering van een logisch circuit in een mijnenvegerbord) om te bewijzen dat Minesweeper Inference co-NP-volledig is. Minesweeper Inference is dus bij de moeilijkste problemen in co-NP.

Maar kunnen we beide resultaten (de NP-volledigheid van Minesweeper Consistency en de co-NP-volledigheid van Minesweeper Inference) nu niet van elkaar afleiden? Het zou toch erg stom zijn als we de volledige constructie helemaal opnieuw moeten doen, voor twee resultaten die zoveel op elkaar lijken.

Wel... stel dat je Minesweeper non-Inference wilt reduceren tot Minesweeper Consistency (zodat de NP-volledigheid van Minesweeper Consistency zou volgen uit de co-NP-volledigheid van Minesweeper non-Inference). Dat lijkt redelijk gemakkelijk. Je kan niets afleiden als en slechts als voor elk nog verhuld vakje zowel de toestand "bom" als "geen bom" consistent is. Die verschillende consistentie-vragen kan je gemakkelijk samenvoegen tot het consistentieprobleem voor één groter bord... behalve dat "geen bom" niet bestaat als toestand! Als er geen bom ligt op een vakje, dan bevat het vakje een getal, het aantal omliggende bommen. Aldus moeten we een disjunctie maken over de verschillende mogelijke aantallen van elk vakje, maar dat kan niet zomaar met een many-one reductie, het soort van reductie waarmee NP-volledigheid normaal gezien gedefinieerd wordt. Het werkt dus niet... en dat was dan nog de intuïtief gemakkelijkere richting.

Moest het bovenstaande wel werken, dan zou het artikel van Scott, Stege en Van Rooij sterker zijn dan Kaye's artikel, en dus een echte verbetering. Nu is het echter niet zozeer sterker, gewoon een andere nuance. Het algemene beeld wordt er eerder minder aantrekkelijk op. Het ziet ernaar uit dat er een hele hoop mijnenvegerproblemen bestaat, allemaal op zichzelf NP-volledig of co-NP-volledig, maar niet met natuurlijke, intuïtieve reducties naar elkaar te herleiden. Tenzij je flexibeler bent me je reducties: niet enkel many-one, maar bijvoorbeeld Turing reducties waarbij de orakels enkel positieve antwoorden geven (om toch maar het onderscheid te behouden tussen NP en co-NP) en waarbij je verschillende orakelvragen tegelijk kunt stellen. Dat lijkt mij sterk genoeg om natuurlijke reducties te krijgen tussen alle mijnenvegerproblemen. Weet er iemand of dit soort reducties bestudeerd wordt in complexiteitstheorie? Het zou leiden tot een zwakker begrip van NP-volledigheid, maar het lijkt me toch nog interessant.

Conclusies voor de casual gamer

Genoeg technische jibber-jabber nu. Welke conclusies moet de niet-wiskundige mijnenveger-liefhebber nu uit dit alles trekken? Wel, stel dat je vast zit en niet meer weet of je nog iets logisch kunt afleiden, dan wel moet gaan gokken. Bestaat er een efficiënt algoritme dat je kan vertellen of je nu echt moet gokken of niet? Wel, voor kleinere borden is het misschien nog wel doenbaar, maar verwacht je niet aan een algoritme dat ook voor grotere mijnenvelden efficiënt blijft. Als je toch werkelijk zo'n algoritme gevonden hebt, dan heb je P=NP bewezen en ben je en miljoen dollar rijker.

Stel nu dat er een helderziende vriend over je schouder staat mee te kijken. Hij beweert het antwoord te weten op de vraag of je nu moet gokken of niet. Kan hij je overtuigen dat hij werkelijk het juiste antwoord heeft, en geen charlatan is? Dat hangt af van zijn antwoord. Als hij beweert dat je niets meer logisch kunt afleiden, dan kan hij je daar gemakkelijk van overtuigen met het certificaat waar ik eerder over sprak. Maar, verrassend genoeg: als hij beweert dat je nog wel iets logisch kunt afleiden, dan heeft hij in het algemeen géén manier om je daar snel van te overtuigen! En als hij dat toch altijd kan, dan heeft hij co-NP=NP bewezen, terwijl de meeste wetenschappers juist vermoeden dat co-NP en NP verschillende klassen zijn.

Wat ook het geval is, er blijft altijd een fundamenteel probleem over met mijnenveger. Je zult altijd situaties hebben waar je wel moet gokken. Dan heb je net een hele week gewerkt om een 1000x1000-mijnenveld voor 99% op te vegen, bij het laatste stukje moet je gokken en BOEM! Dood... Dergelijke frustraties zijn intrinsiek aan mijnenveger. Daar kan geen complexiteitstheorie verandering in brengen.

Aldus is het misschien beter om mijnenveger maar te vergeten, en bijvoorbeeld te bestuderen waarom ladders in het bordspel Go PSPACE-moeilijk zijn? Dat is echter voor een andere keer...

PS: voor wie meer wil lezen over complexiteitstheorie en NP-volledigheid: het boek "Computers and Intractability" van Garey en Johnson is reeds meer dan 30 jaar oud, maar nog steeds fantastisch leesmateriaal.